衡水名师卷·2022-2023学年度高三分科检测提分卷·151靶向提升(老高考)历史(三)3试题 答案

衡水名师卷·2022-2023学年度高三分科检测提分卷·151靶向提升(老高考)历史(三)3试题 答案，目前全国100所名校答案网已经汇总了衡水名师卷·2022-2023学年度高三分科检测提分卷·151靶向提升(老高考)历史(三)3试题 答案的各科答案和试卷，更多全国100所名校答案请关注本网站。

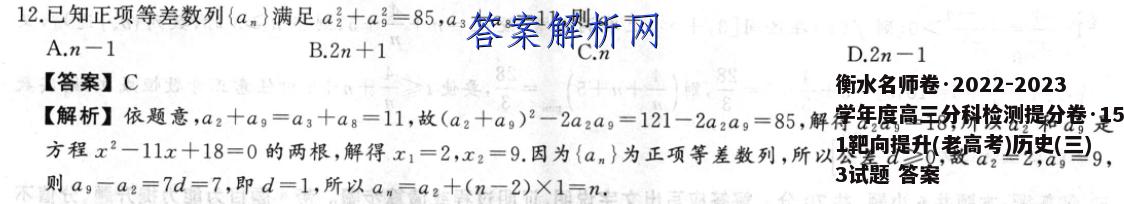
12.已知正项等差数列{am}满足a十a?=85,a3十ag=11,则am=A.n-1B.2n+1C.nD.2n-1【答案】C0【解析】依题意，a2十ag=a3十ag=11,故(a2十ag)2-2a2ag=121-2a2ag=85,解得a2ag=18,所以a2和ag是方程x2一11x十18=0的两根，解得x1=2,x2=9.因为{am}为正项等差数列，所以公差d≥0，故a2=2,ag=9,则ag-a2=7d=7,即d=1,所以am=a2十(nT2)X1元n,女台*若数列{am}中不超过f(m)的项数恰为bm(m∈N·),则称数列{bm}是数列{am}的生成数列，称相应的函数f(m)是数列{an}生成{bm}的控制函数.已知an=2n,且f(m)=m,数列{bm}的前m项和为Sm,若Sm=30,则m=的中年容的：。A.9B.11C.12D.14【答案】B【解析】由题意可知，当m为偶数时，可得2m≤m,则6.-贺：当m为奇数时，可得2n≤m-1,则b.=m2,所m-12,m=2k-1,以bm=EN),则当m为隔数时S.=61+b:十…+b.=号1+2+…十m)号×号2,m=2k∈N,所以无解；当m为寺数时，S。=b1十6，十(m+1)24m+1_m2-2,所以m1=30,因为m∈N,所以m=11

*已知等比数列{am}的前n项和Sm=a十3c(a,c∈R,c≠0，c≠1).(1)求实数a的值；(2②)若c=号，且6.=。，则当n取何值时，6，}取得最小值，并求此最小值。解：(1)当n≥2时，am=Sm-Sm-1=a十3c-a-3c"-1=3(c-1)cm-1,所以am+1=3(c一1)c"（米).则am+1=Cam·当n=1时，a1=S1=a+3c,因为{an}为等比数列，所以a2=a1·c=(a十3c)c.由(*)式可知，a2=3(c一1)c,所以3c(c-1)=c(a十3c),解得a=一3.2当6=时a=×(所以6.-品×)1D×◆6n≥动即D×(停》≥×()，解得2≥4，令616，解得a b2>b3>b4=b5